Fraunhofer Institute for Mechanics of Materials IWMThe physics of fluids and granular media in combination with efficient numerics constitute the heart of SimPARTIX®.
The power within: physics and numerics
Jump to:
Discrete element method (DEM)
Contact between two DEM particles each consisting of several spheres (left) and a schematic presentation of a contact event (right).
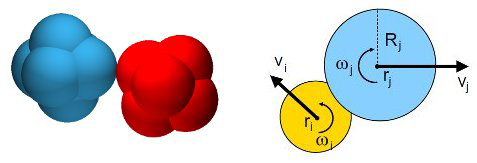
Spheres represent a reasonable first approximation for modeling individual particles; agglomerates of spheres can be used to model individual particles with more complex forms. Various physical interactions occur between the particles. For example, repulsion is modelled by Hertzian contact stresses or harmonic restoring forces, cohesion by the Johnson-Kendall-Roberts theory while taking into account the surface energy, friction is taken into account in the simulation in the form of Amonton’s law, and dissipation of kinetic energy is described by collisions. The aforementioned mechanisms occur only in the case of direct contact between the particles. But long-range interactions can also be taken into account, e.g. those between electrically charged or magnetic particles. Ultimately, all interactions cause forces that have effects on the individual particles. The motion of the particles is then described by Newton’s laws.
Further reading:
T. Pöschel, T. Schwager. Computational Granular Dynamics. Springer, 2005.
Smoothed particle hydrodynamics (SPH)
Simulation of a dam failure with SPH (top) and reconstruction of the surface of the fluid for correct visualisation (bottom).
The behavior of fluids can be described by the Navier-Stokes equations, which are absolutely fundamental to fluid mechanics and represent a generalisation of Newton’s laws for continuous media. This particle-based method consists of dividing the volume to be simulated into particles, or rather “fluid lumps”, and converting the Navier-Stokes equations into motion equations for these particles, an approach that allows free surfaces and multi-phase flows to be readily considered. Complex rheological behavior such as shear thinning or thixotropy can be taken into account by modifying the interactions of the fluid lumps. Suspensions can be modelled explicitly by allowing the dispersed solids in the liquid to interact with the lumps. Furthermore, it is also possible to model flexible walls (fluid-structure coupling) as well as rigid walls. The associated deformation is modelled with elastic or plastic material laws.
Further reading:
J. J. Monaghan. Smoothed particle hydrodynamics. Reports on Progress in Physics, 68(8):1703–1759, 2005.
Time integration and boundary conditions
Schematic diagram of a simulation box with periodic boundary conditions. If a particle exits the box at the top, another particle enters the box at the corresponding point at the bottom.
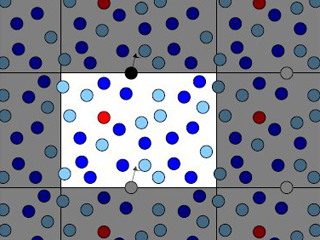
Both the discrete element method and smoothed particle hydrodynamics are dynamic numerical methods, which means that the forces, or rather accelerations, involved must be converted into changes in the positions and velocities of the particles. This is achieved through explicit time integration using the efficient velocity-Verlet algorithm with an adaptive time step.
A multitude of three-dimensional boundary conditions are available for the simulation. In some applications it may be sufficient to model just one representative part of the system with periodic boundary conditions in one, two or three dimensions. Purely two-dimensional simulations are also possible. Shear fields – in those applications where they occur – can be taken into account with the help of the so-called Lees-Edwards boundary conditions.
Further reading:
M. P. Allen, D. J. Tildesley. Computer Simulation of Liquids. Oxford University Press, 1987.
Parallelization
Particles at the boundary between the computational domains must be exchanged between processors in order to guarantee the correct interaction across the boundary.
Depending on the particular issue, a high detail resolution may be desirable for the application under examination. In some instances this can lead to a very large number of particles needing to be considered. Parallel simulations can be used to obtain results quickly despite this effect. To do this, SimPARTIX® makes use of domain discretization. The simulation volume is divided into equal segments. Each processor then performs the simulation for a particular segment (domain). The processors communicate with each other in order to guarantee the correct interactions at the boundaries between the domains. Parallelization can be spread over a handful of computer cores, which are available in current multicore architectures, or over several hundred high-performance computers.
Further reading:
S. Plimpton. Fast parallel algorithms for short-range molecular dynamics. Journal of Computational Physics, 117(1):1–19, 1995.