Fraunhofer Institute for Mechanics of Materials IWMMaterials modeling
Options
Elastic or plastic material deformations are the response of a work piece due to strong external forces on the work piece. If a critical deformation limit is exceeded, ductile or brittle failure mechanisms are initiated. The quantitative description of the deformation and failure behavior of different materials allow the optimization of a wide range of industrial applications.
During the wire sawing process in the solar industry, the silicon ingot is cut into silicon wafers using abrasive diamond particles.
The abrasive waterjet cutting uses abrasive particles in a stream of water in order to cut precise geometries under high pressure.
In the finishing stages of industrial products that possess hardly accessible surfaces, the process of abrasive flow machining (AFM) is applied. For this, a viscous medium, enriched with highly abrasive particles, is forced to flow along the work piece surface, and thereby achieving a polishing effect due to the abrasiv removal of material.
These are some examples of processes that are based on the effect of abrasive particles on the component material, where an appropriate degree of removal is desired. In other situations, it is critical to reduce wear, and thus to reduce material removal due to abrasion or erosion. With SimPARTIX® simulations, it is possible to analyze these processes in detail at the level of the individual abrasive particles. Thereby, we can derive hints for the optimization of the process parameters or the geometry of the component part.
Plasticity and ductile failure
An abrasive grain (red) removes material from a ductile workpiece (blue) (from Takaffoli et al., Wear, 274–275:50–59, 2012).
Comparison of the crater profile from the SimPARTIX® simulation and the experiment (from Takaffoli et al., Wear, 274–275:50–59, 2012).
The simulation of processes involving large deformations and high shear rates poses great challenges to the simulation tool. Nonetheless, numerical simulations are essential for a deeper understanding of the processes, which subsequently enables process optimization. By using a numerical model, the plastic deformation and the damage of the processed material is to be predicted.
The advantage of the particle-based method lies in the mesh-free approach. This approach allows to simulate damage and large plastic deformations in a natural way. The deformation or crack formation is not determined by the choice of the grid, but results from the motion of the particles.
For the simulation of ductile damage processes the plastic deformations and the failure of the material must be accurately reproduced by the numerical model. In SimPARTIX®, the plastic deformations of the workpiece are modeled using a Johnson-Cook plasticity model for the von Mises yield stress. At high strain rates, the Cowper-Symonds equation is used, which specifies the yield stress at high strain rates as a function of the strain rate and of the yield stress under quasi-static conditions. For the failure of the material at high strains, the Johnson-Cook failure criterion is used, which predicts the fracture of the material at a certain plastic deformation under dynamic loading.
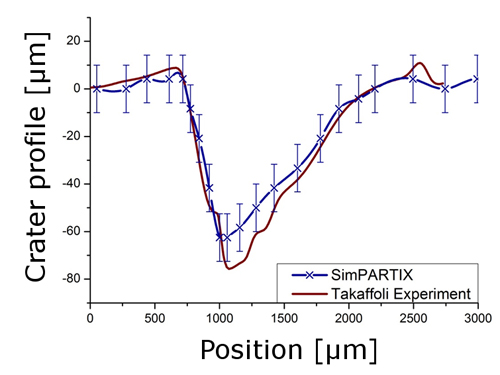
The figure shows the simulation of an abrasive grain hitting a workpiece. The workpiece is plastically deformed by the abrasive grain and a chip is formed. Above a certain plastic strain, the material fails and the chip can be removed from the surface of the workpiece.
SimPARTIX® simulations are used in the design layout of components and in the derivation of optimal process parameters.
Case study: Abrasive machining
Brittle fracture
Simulation of a three point bending test with a brittle material.
Ceramics or glasses typically show brittle fracture behavior. Under tensile stresses these materials show an elastic behavior with reversible deformations. Above a certain tension threshold, however, these materials fail instantly with a complete relaxation of the applied stresses. The resulting breaking edge of crystalline materials is usually oriented along the crystal lattice structure showing smoothness at the atomic scale.
The fracture toughness of a brittle material is quantitatively described by a critical stress intensity factor. This quantity is an upper bound for the applied tension at the tip of an evolving crack. Once this bound is exceeded, brittle fracture occurs.
In SimPARTIX® the mechanics of brittle fracture are modelled by the theory of peridynamics, which is a non-local extension of the classical continuum mechanic formalism. The mathematical structure of the peridynamic theory is well suited for the application in particle-based simulation techniques. Each single particle represents a finite volume of the work piece, which is connected to the neighboring particles by force bonds, whose stiffness represents the compressibility of the material. The fracture toughness of the material is then described by a critical limit of the deformation of the force bonds. If this limit is exceeded, brittle failure is initiated.
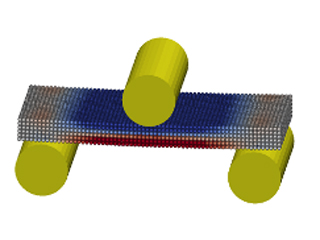
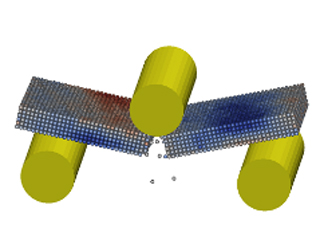
Simulation of a three point breaking test of a silicon crystal. The upper cylinder is pushed downward in a path-controlled trajectory. On contact, the induced stresses on the upper and lower surface are discernible. Eventually, brittle failure of the silicon crystal is initiated.